Judaism 101
Judaism 101
Level: Intermediate
The basics of the Jewish calendar were explained on the Jewish Calendar page, and will be mentioned only in passing here. This page is intended for those who are interested in a deeper understanding of the workings of Rabbi Hillel II's fixed calendar, or those who want to be able to write their own code to build a Jewish calendar or calculate a Jewish date.
Although this page will focus primarily on calendar calculations, I encourage you not to dismiss this as purely a mathematical exercise devoid of spiritual value. The sages emphasized the value of studying astronomy as a way of appreciating the greatness of the Creator's work. This page does focus on some arcane mathematics, but do not be intimidated by it: the Jewish scholar Rambam wrote that, "the method of the fixed calendar is one which an average school child can master in 3 or 4 days." (Hilkhot Qiddush HaChodesh 11:4). A lot of the confusion people experience stems from variations in the way different sources say the same thing, and the way some sources use familiar terms to mean unfamiliar things. I will do my best to keep these variations straight for you. Also, Rambam's schoolchild was probably using a calculation shortcut that will be discussed later, but as with basic mathematics, you should learn the underlying principles before you rely on a shortcut.
This page includes JavaScript that performs all of the calculations described, in the order that the concepts are presented here and with detailed comments. Those who are comfortable with programming languages may find it faster and easier to understand the math by looking at the code. This code is not necessarily the best or most efficient script possible, but it's not intended to be; it's intended to illustrate how the calendar is calculated.
The Jewish calendar is based on three astronomical phenomena: the rotation of the Earth around its axis (a day); the revolution of the moon around the Earth (a month); and the revolution of the Earth around the sun (a year). These three phenomena are independent of each other, so there is no direct correlation between them. On average, the moon revolves around the Earth in about 29½ days (a lunar month). The Earth revolves around the sun in about 365¼ days, that is, about 12 lunar months and 11 days.
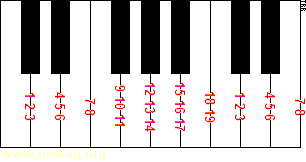
To coordinate these three phenomena, and to accommodate certain ritual requirements, Rabbi Hillel II developed a fixed calendar in the Jewish year 4119 (about 358 on the secular calendar). His calendar, still in use today, consists of 12 or 13 months of 29 or 30 days, and can be 353, 354, 355, 383, 384 or 385 days long. A 13-month year is referred to in Hebrew as Shanah Me'uberet (שָׁנָּה מְעוּבֶּרֶת, shah-NAH m'-oo-BEH-reht), literally: a pregnant year! In English, we just call it a leap year. Leap years occur in 19-year cycles, in the 3rd, 6th, 8th, 11th, 14th, 17th and 19th years of the cycle. These cycles start with creation, so you can just divide the year number by 19 and the remainder (using the modulus operator for you programmers) is the year of the cycle. I am writing this in 5784, which is the 8th year of a cycle and is a leap year. Next year (beginning in October 2024) is the 9th year of the cycle, which is not a leap year. If you are musically inclined, the cycle of leap years can be remembered by the black keys on a piano keyboard, though this is easier to understand if you can see it, as below.
The keystone of the calendar is the new moon, referred to in Hebrew as the molad (מוֹלָד, pronounced moh-LAHD). Molad is the Hebrew word for birth and refers more or less to what we call the "new moon" in English. The difference is: astronomical new moon occurs when the moon is not visible to the naked eye, while the molad occurs a day or two later, when the moon first becomes visible again (the "crowning" in the "birth" of the new moon).
The molad for the month of Tishri is the most important one for calendar calculations, and is referred to as Molad Tishri. Tishri is the month when the calendar year number changes, on the festival of Rosh Hashanah, though it is actually considered the seventh month of the year (month count starts in Nissan, the month of Passover). Rabbi Hillel's calendar requires Rosh Hashanah to fall on a Monday, Tuesday, Thursday or Saturday for ritual reasons. If it fell on Wednesday or Friday, then the major fast of Yom Kippur (the 10th day) would fall on a Friday or Sunday (the day before or after Shabbat), which would interfere with planning for or observing Shabbat. If Rosh Hashanah fell on a Sunday, the Hoshanah Rabbah (the 21st day) would fall on a Shabbat, making it impossible to observe some of the day's customs.
Note that the calculated molad does not necessarily correspond precisely to the physical phenomenon. The length of time from one astronomical new moon to the next varies somewhat because of the eccentric orbits of the Earth and Moon; however, the moladot of Rabbi Hillel's calendar are set using a fixed average length of time: 29 days, 12 hours, and 793 "parts" (or in Hebrew, חַלַקִים, chalakim). The amount of time is commonly written in an abbreviated form: 29d 12h 793p.
A "part" (or in Hebrew, חֵלֶק, cheilek, the singular form of chalakim) is a unit of time used in the Jewish calendar, equal to 3 and 1/3 seconds. There are 18 parts in a minute and 1,080 parts in an hour. Most sources express time from calendar calculations in days, hours and parts, although some sources break the parts down into minutes. For example, the period between moladot could be written as 29 days, 12 hours, 44 minutes and 1 part (29d 12h 44m 1p), because 793 parts is 44 minutes and 1 part (793 = 44 minutes x 18 parts + 1 part) . This makes the resulting times look somewhat more familiar, but it increases the number of calculations, so I usually stick with days, hours and parts.
The same shorthand can be used to express the time when a molad occurs. The time is normally expressed as a day of the week, along with the hours and parts (or hours, minutes and parts). For example, the time of a molad might be expressed as 2d 12h 1005p (or 2d 12h 55m 15p), meaning that it occurs on Monday (the second day) at the 12th hour and 1005 parts.
The hours used to calculate the molad are standard 1/24 of a day hours. Note that this differs from the "seasonal hours" used for ritual scheduling, which are 1/12 of the time from sunrise to sunset. For example, at Passover, we are required to stop eating chametz at the end of the "fourth hour" of the morning on Nissan 14, that is, at the end of 1/3 of the time between sunrise and sunset. These seasonal hours vary depending on the time of the year and your location: seasonal hours in Alaska in winter are much shorter than seasonal hours in Florida at the same time (Alaska daytime is shorter). Summer seasonal hours in both locations are longer than winter seasonal hours. But molad hours are constant, 1/24th of a day. The time for the molad is Jerusalem Solar Time, which is not necessarily the same as your local time. It is also not necessarily the same as the time on the clock, even in Jerusalem. This fact has no effect on your calculations, but is worth knowing.
The Jewish "day" starts at sunset, rather than at midnight. If you read the story of creation in Genesis Ch. 1, you will notice that it says, "And there was evening, and there was morning, one day." From this, we infer that a day begins with evening, that is, at sunset. Accordingly, most sources discussing the molad use 6PM of the previous secular day as the "zero hour." In our example, 2d 12h 1005p, the 12h means the 12th hour after 6PM Sunday, that is, 6AM Monday. If a molad occurs at 2d 4h 0p, this means that it occurs at 10PM on Sunday night, because the second day (Monday) begins at 6PM on the secular Sunday.
Some sources, however, use the more familiar Western conventions and use midnight as the zero hour. The 2d 12h 1005p I gave above (6AM Monday) would be written 2d 6h 1005 while the 2d 4h 0p (10PM Sunday) would be written 1d 22h 0p, which is certainly more familiar but as we will see it confuses other pieces of the puzzle. If you get a molad time from another source, be very careful to check which system is being used! If the time is referred to as "Rambam time" or something similar, then you know it uses 6PM as the zero hour. On this page, I am using Rambam time, but some well-respected Orthodox sources in America use midnight as their zero hour. As long as you are consistent, you will get the same result under either system.
We've seen that a year can start on one of four different days (Monday, Tuesday, Thursday or Saturday), that it could be a leap year or a regular year, and leap and regular years each have three possible lengths (353, 354 or 355 days in a regular year; 383, 384 or 385 days in a leap year). The combination of these three pieces of information is referred to as the keviya (קְבִיעַ), literally translated as "determined" or "fixed" or "appointment," but I like to think of it as a "setting" for the year. If we know the keviya, we know everything we need to know about the calendar for the year. We could have an entire Hebrew calendar prepared for each keviya, with every holiday (major and minor, including ones that are moved because of Shabbat), every Torah and Haftarah reading, every observance, birthday and yahrzeit. The only thing that changes from year to year is the Hebrew year number and the secular date (which doesn't match up with the Hebrew calendar at all!). The layout of the calendar would be exactly the same for every year that has the same keviya.
Theoretically, there could be 24 different possibilities for the keviya (4 start days x 6 lengths), but because of the way the calendar calculations work, only 14 of those combinations can ever actually happen. Interestingly, the secular calendar also has 14 possible layouts (7 start days x 2 lengths), but that's just a coincidence, the two systems do not correspond to each other in any way.
Calendar scholars use a system to identify each keviya, a set of codes that provides basic identifying facts about the year. There are actually several different systems of encoding the keviya, but the ones I've seen are all two or three letter codes. Once the keviya is known, your Hebrew calendar is essentially built. There are three basic systems I have seen (explained in more detail below):
The third system was the first one I learned and it's the one I prefer but the programming languages I use aren't fluent in Hebrew so I've started programming with the first one. They all ultimately get the same results if you use them consistently.
A little more information about how all of this gets coded:
The weekday for Rosh Hashanah or Passover could be represented as an Arabic numeral or a Hebrew letter. Letters of the Hebrew alphabet have numerical values and can be used as numerals (see Hebrew Alphabet).
The letters used for Rosh Hashanah are Beit for Monday (ב, value 2), Gimmel for Tuesday (ג, value 3), Hei for Thursday (ה, value 5) or Zayin for Saturday (ז, value 7). Rosh Hashanah can only fall on these days, as discussed above.
Passover can fall on any day of the week. If using a coding system that gives the Passover day as a Hebrew letter, use Alef for Sunday (א, value 1), Dalet for Wednesday (ד, value 4) or Vav for Friday (ו, value 6).
The months of Cheshvan (October/November) and Kislev (November/December) can be either 29 or 30 days. Cheshvan is normally 29 days and Kislev is normally 30, giving a 354 or 384 day year. If the year uses these normal lengths, it is referred to as K'Seder (in order or regular) and is represented with the Hebrew letter Kaf (כ) or the Latin letter R (for Regular).
If Kislev is 29 days, giving a 353 or 383 day year, it is referred to as Chaseir (deficient or lacking), and is represented with the Hebrew letter Cheit (ח) or the Latin letter D (for Deficient).
If Cheshvan is 30 days, giving a 355 ot 385 day year, it is referred to as Shaleim (whole or complete), and is represented with the Hebrew letter Shin (ש) or the Latin letter F (for full) or C (for complete).
If the system explicitly codes the leap year it uses the Hebrew letters Pei (פ) or Mem (מ). Pei stands for the Hebrew word P'shuta (פְּשׁוּטָה, simple), and refers to a 12-month regular year. Mem stands for Me'uberet (מְעֻבֶּרֶת, pregnant!), and refers to a 13-month leap year.
As I said before, the two-digit system that uses Latin letters uses a capital letter for the year length when the year is a leap year and lower case when it is not, which I think is a very convenient and interesting way to code it.
Conveniently, each piece of this system uses different Hebrew letters, making it easier to know what's going on even if you come across a different system than you are used to!
When I first started writing about the keviya, the Hebrew year was 5783, which was a non-leap year that started on a Monday, had 30 days in Cheshvan and observed Passover on a Thursday (Wednesday night). The three systems above might encode the keviya this way:
Note that the two letters of the first one correspond to the first two letters of the second one (the ones on the right, because Hebrew is right-to-left) and the last two letters of the third one (the ones on the left). They all refer to the same thing.
One of the powerful things about these encodings is that they correspond to the distribution of weekly Torah readings. For example, in the year 5783, on 3 Nissan (March 14, 2023), the Torah portion was Vayiqra. The next year of this keviya will be 5800 (2039/2040), and the same reading will be read on 3 Nissan of that year, though it will be March 17, 2040. Contrast this with the next year, 5784 (keviya 7D מזח זחג), when Vayiqra was read on 13 Adar II, practically Purim, along with a reading for Shabbat Zachor, a Purim-related reading that was not read with Vayiqra in 5783.
The following table shows which parshiyot are combined in which year encodings, showing all three encoding formats:
| Keviya | Vayaqhel Pequdei | Tazria Metzora | Acharei Mot Qedoshim | Behar Bechukotai | Chuqat Balaq | Mattot Masei | Nitzavim Vayeilekh* | |
|---|---|---|---|---|---|---|---|---|
| LEAP | 2D מבח בחה | X | X | X | ||||
| 2F מבש בשז | X | |||||||
| 3R מגכ גכז | X | |||||||
| 5D מהח החא | ||||||||
| 5F מהש השג | X | |||||||
| 7D מזח זחג | X | X | ||||||
| 7F מזש זשה | X | X | X | |||||
| SIMPLE | 2d פבח בחג | X | X | X | X | X | X | |
| 2f פבש בשה | X | X | X | X | X | X | X | |
| 3r פגכ גכה | X | X | X | X | X | X | X | |
| 5r פהכ הכז | X | X | X | X | X | |||
| 5f פהש השא | X | X | X | X | ||||
| 7d פזח זחא | X | X | X | X | X | |||
| 7f פזש זשג | X | X | X | X | X | X |
*Nitzavim and Vayeilekh are among the last readings from the Torah, before the readings restart three weeks after Rosh Hashanah. When these readings are combined, they are read before Rosh Hashanah, in the year specified. When they are split, Nitzavim is the Shabbat before Rosh Hashanah and Vayeilekh is after Rosh Hashanah, in the following year.
As I said, the calendar revolves around the date of Rosh Hashanah, the first day of the year, and the new moon of that month, the Molad Tishri. Once the Molad Tishri is known, there are various rules that postpone the date or Rosh Hashanah a day or two. There is a simple table, known as the Four Gates, that tells you the keviya for the year including the day of Rosh Hashanah, but you still have to calculate the Molad Tishri to use the table and it's worth knowing what's going on under the hood here.
We will now look at these steps in detail. I won't bore you with the mathematics, but if you're a geek like me and interested in that sort of thing, you can see the code here. This code is designed to illustrate calendar principles and is not the most efficient code possible, but it is very straighforward and has extensive comments. The form below uses the functions in that Javascript file to calculate the date of Rosh Hashanah for any Hebrew year after 5731 (1970/71).
Step 1: Start with a Known Molad
To perform any calculations on the Jewish calendar, you need a starting point, the molad of Tishri for a specific year, along with the corresponding secular date if you want to be able to convert the Hebrew date to secular. It is not possible to work out a molad from first principles, because the first molad of creation (known as Molad Tohu, from the phrase in Genesis 1:2, tohu va-vohu, unformed and void) did not occur at 0d 0h 0p!
I like to base my calculations on the molad of Tishri 5732, which occurred at 2d 7h 743p (using 6PM as the zero hour), and corresponded to the secular date September 20, 1971. I like this particular year because it is the first Molad Tishri after January 1, 1970 (Javascript's 0 date) that is not subject to dechiyot (postponements that we will learn about later), which complicate secular date conversions. If you will be calculating dates in the past and would like to avoid the complications of subtracting dates, you may prefer to work with an earlier molad, such as:
I'm sure our Christian friends are primarily interested in knowing Molad Tishri 3762 (the year 1), or some other year in that lifetime. Unfortunately, these calculations would be meaningless because that was more than 350 years before this calendar was created, and at that time new months and leap years were determined by observation, not by calculation, which could give somewhat different results. In addition, it is very complicated to convert a Hebrew date to a secular date before the Gregorian calendar reforms, which took effect at different times in different countries: it was introduced and adopted in Catholic countries in 1582 but not adopted in America until 1752! In the Russian Empire, where many of our Jewish ancestors were born, it wasn't adopted until after the Soviets took over in 1918! No wonder they didn't know their secular birthdays!
Step 2: Determine the Number of Months to Tishri of Your Year
The next step is to determine how many months are between your starting year and the year you want. There are exactly 235 months in every 19-year cycle of leap years (12 12-month years plus 7 13-month years), but if your number of years is not evenly divisible by 19, then you will have to determine whether each remaining year is a regular year (12 months) or a leap year (13 months).
As discussed above, to find out if a year is a leap year, you get the remainder after dividing the year number by 19. If the remainder is 3, 6, 8, 11, 14, 17 or 0 (the 19th year of the cycle) then the year is a leap year. Otherwise, it is not.
Step 3: Multiply the Number of Months by the Length of the Molad
Next, you multiply the number of months by the average length of the molad, which is 29d 12h 793p to determine the elapsed time. Of course, you will then have to round up the smaller units into the larger units, just as we would round 75 minutes into 1 hour and 15 minutes.
Step 4: Add the Elapsed Time to the Starting Molad
Some of this may seem duplicative because we're going to have to do some rounding again, but I like to keep this separate to be very clear about distinguishing between the elapsed time and the day of the week. The "day" part of the starting molad is a day of the week, not elapsed time. If you know that Passover starts on Thursday (5th day) April 2 and lasts 8 days and you want to know what date it ends, you don't add 5 (the starting day of the week) to the 8! I'm sure there are more efficient ways to handle this, but the point is, don't mix up the days elapsed with the day of the week!
Step 5: Apply the Dechiyot (דְּחִיוֹת)
There are four rules of postponement known as dechiyot (דְּחִיוֹת), pronounced d'-khee-YOHT, where "kh" is a throat-clearing noise (singular: dechiyah, דְּחִיָה). These rules postpone the date of Rosh Hashanah, but do not affect the calculated time of the molad. One of the dechiyot is a general rule of rounding while the rest are designed to prevent oddities in the length of the year and the date of Rosh Hashanah.
These rules push the new year's date out by adding a day to the previous year's months of Cheshvan or Kislev. To know everything you need to know about a calendar year, you would need to calculate the current Rosh Hashanah (to know when it starts) and the following year's Rosh Hashanah (to know the length of Cheshvan and Kislev, two months very early in the year). Scholars figured out a long time ago that this was unnecessarily complicated so they developed a simple table that tells you, from the year's Molad Tishri, everything you need to know about the year. We will discuss this soon and no one manually calculates the dechiyot any more, but it's worth knowing what they're doing and why they're doing it.
These dechiyot can add one or two days to the elapsed time, but we'll see how that is handled when we get to the Four Gates table
Dechiyah 1: Molad Zakein
The first dechiyah is molad zakein, meaning an "old" molad. If the molad occurs at or after noon (that is, 18h where 6PM is 0h or 12h where midnight is 0h), the molad is considered to be "old" and we round to the next day. This rule is quite commonly applied, affecting a quarter of all years (half if you use midnight as the 0 hour).
If noon seems a bit early to be considering the molad "old," remember that the Jewish "day" starts at sunset. The rule of molad zakein simply means that a molad at or after noon relates to the "day" that starts at the next sunset (4-10 hours later) rather than the previous sunset (14-20 hours earlier). This rationale is clear from the Rambam notation, where 6PM is 0h and a Molad Zakein is one that occurs at or after 18h in a 24h day.
Dechiyah 2: Lo A"DU Rosh
The second dechiyah is known as Lo A"DU or Lo A"DU Rosh. This is the rule that
preventsRosh Hashanah from fallingon a Sunday (Day 1), a Wednesday (Day 4) or a
Friday (Day 6). The word Lo means "Not," and the word A"DU is a way of pronouncing Alef-Dalet-Vav, letters
with the numerical values 1, 4 and 6 (see Hebrew Alphabet - Numerical
Values). If the calculated molad occurs on one of these days of the week, Rosh Hashanah is postponed by a
day to prevent other problems with the calendar mentioned above.
This dechiyah is also commonly applied, as you might imagine. It applies to three out of seven days, so one would expect it to occur almost half of the time.
Note that the dechiyot of molad zakein and Lo A"DU Rosh can work in combination, with molad zakein applied first: a molad at 5d 19h 0m 0p (Thursday at 1PM) is rounded to Friday by the rule of Molad Zakein, then postponed to Saturday by the rule of Lo A"DU Rosh, even though the original molad was on a valid day of the week. On the other hand, a molad at 4d 19h 0m 0p (Wednesday at 1PM) is rounded to Thursday by Molad Zakein, and Lo A"DU Rosh does not apply: even though the molad occurred on Wednesday, Molad Zakein has already moved it off of that date so Lo A"DU Rosh is not necessary.
Dechiyah 3: Gatarad
The remaining two dechiyot are much less commonly applied.
Dechiyah Gatarad holds that if Molad Tishri in a simple (12-month, non-leap) year occurs on a Tuesday at 9h 204p or later, Rosh Hashanah is postponed to the next day (a Wednesday, which by the effect of Lo A"DU Rosh would then be postponed to Thursday).
The
name, Gatarad, is a mnemonic for the rule. In Hebrew, Gatarad it is spelled Gimel-Teit-Reish-Dalet. Using
letters as numerals, Gimel is 3, and represents Tuesday. Teit is 9 and represents the 9th hour (that is, 9h
in Rambam notation, but 3h in midnight-based notation). Reish is 200 and Dalet is 4, representing 204 parts.
Why does such a complicated rule exist? This rule prevents the possibility that a year might be 356 days, an invalid length. Consider: a Molad Tishri at 3d 9h 204p would not be postponed by Molad Zakein or Lo A"DU Rosh. Add 12 lunar cycles (354d 8h 876p) to the next year's Rosh Hashanah and you get 7d 18h 0p with 354 days elapsed. Molad Zakein applies to the following year, postponing Rosh Hashanah to the next day, a Sunday, with 355 days elapsed. Lo A"DU Rosh is then triggered, postponing Rosh Hashanah and leaving 356 days elapsed and making the current year an invalid length. Gatarad takes two days away from the current year (starts the year two days later) and adds them to the preceding year, so both years are a valid length.
Note that this rule is not combined with Molad Zakein. If Molad Zakein applies to the current year, Gatarad is unnecessary; thus Gatarad applies only to molads between 9h 204p and 17h 1079p.
As you might imagine, this rule is not commonly applied. It applies only in non-leap years (12 out of 19 years) when the molad occurs on Tuesday (1 out of 7 days) between the 9th hour and the 18th hour (9 out of 24 hours). It occurs about three times a century. It last occurred in 5745 (1984-85) and will not occur again until 5796 (2035-36).
Dechiyah 4: Betutkafot
Like Dechiyah Gatarad, this rule is not very commonly applied and is designed to prevent a year from having an invalid length. Dechiyah Betutkafot prevents a leap-year from having 382 days (too few days) by postponing Rosh Hashanah of the non-leap year following the leap year.
Also
like Dechiyah Gatarad, the name of the rule tells you how it is calculated: if Molad Tishri in a year
following a leap year occurs on Monday (ב, Beit, 2) after the 15th hour
(טו, Teit-Vav, 15 in Rambam notation, but 9h in midnight-based notation) and 589
parts (תקפט, Tav-Kaf-Pei-Teit, 589), then it is postponed to the next day. The
rule is applied only if the actual molad occurs on Monday, not if it is postponed to Monday. Like Gatarad,
the rule really only applies to molads before noon (18h), because Molad Zakein handles the postponements for
molads at or after noon. Unlike Gatarad, Betutkafot does not trigger Lo A"DU Rosh, because Betutkafot
postpones Rosh Hashanah from a Monday to a Tuesday and Tuesday is an acceptable day for Rosh Hashanah.
The reasoning behind this rule is similar to the reasoning behind Gatarad: the 13 lunar cycles of the preceding year are 383d 21h 589p. If this year's Molad Tishri occurs after 2d 15h 589p, then the preceding year's Molad Tishri must have occurred on or after 3d 18h 0p. This is 384 elapsed days, but the preceding year's Molad Tishri was a Molad Zakein postponing Rosh Hashanah to Wednesday, which triggers Lo A"DU, moving Rosh Hashanah to Thursday. Those two postponements in the preceding year shorten it to 382 days. Dechiyah Betutkafot postpones the current year's Rosh Hashanah by one day to increase the preceding year to a permissible 383 days.
This is the rarest of the four dechiyot, applying only in the year after a leap year (7 out of 19 years) when the molad occurs on Monday (1 out of 7 days) between the 15th hour and the 18th hour (3 out of 24 hours). It applies once or twice a century. The last time it applied was 5766 (2005-06). It will not apply again until 5877 (2116-2117)!
In the early days of the calculated calendar, to know the length of the months of Cheshvan and Kislev (necessary to know when most other dates and holidays fall because those two months are very early in the year) you would have to calculate Rosh Hashanah for one year with all the dechiyot and do the same for the next Rosh Hashanah and calculate the difference. Fortunately, the rabbis came up with a shortcut to sort all this out in one step once you've calculated the Molad Tishri. Yes, you still have to calculate the Molad Tishri for the year you're interested in, but you don't have to work out the dechiyot and you don't have to calculate the next year and its dechiyot to learn the lengths of Cheshvan and Kislev. Once you have the Molad Tishri, you simply look it up in a table and see what the keviya is, telling you the first day of the year and whether it is a deficient year, a regular year or a complete year as discussed above. The keviya may also tell you whether it is a leap year, though that is easily calculated from the year number and you need to know this to use the table anyway. This table is probably why Rambam thought a school child could learn the calendar in a few days!
This shortcut table is called the Four Gates. "Four Gates" apparently refers to the four types of years referenced in the table: a leap year, a regular year before a leap year, a regular year after a leap year, and a regular year between two leap years. "Four Gates" may also refer to the four possible starting days of Rosh Hashanah, which is one piece of the output of the Four Gates. Some Four Gates tables organize the information as a matrix with the four year types on one axis and the four Rosh Hashanah days of the week on the other axis, though the Rosh Hashanah axis is broken down further because the same Rosh Hashanah date could be in a deficient year, a regular year or a complete year.
I have seen the Four Gates table laid out in a number of different formats but the table below is the format I find easiest to understand and use, and is in fact more or less the basis for my calculation of the current date you see at the top of most pages on this site and my Current Jewish Calendar. To use this table:
That's your keviya! Easy-peasy! Note that to get the secular date, you may have to add a day or two to your
elapsed time if the result changes the day of Rosh Hashanah from the day of the Molad Tishri. That's the main
reason I switched to the 2-digit format with Arabic numerals: easier to just subtract your Molad day number
from the Keviya day number and add that to the Elapsed days. If the subtraction result is negative, the Molad
date was Shabbat so add 2 days to get to Monday. You will never need to subtract any days or add more than
two days. Add this number of elapsed days to the secular date of your starting molad and you have the date of
Rosh Hashanah!
REMEMBER: As I said before, the date calculated is the day part of Rosh Hashanah. Hebrew dates
start at sunset the night before this calculated date, sometimes labeled on calendars as Erev (evening,
equivalent to Eve in English).
In the table below, I display all three of the keviya formats discussed above in the order they are discussed above so you can work with whatever keviya format you prefer. The column headings specify the year of the cycle as the remainder when you divide the year number by 19, so you can easily see which column applies to your year.
| Leap Year (0 3 6 8 11 14 17 19)
Molad
Keviya
|
Before Leap (2 5 10 13 16)
Molad
Keviya
|
Between Leap (7 18)
Molad
Keviya
|
After Leap (1 4 9 12 15)
Molad
Keviya
|
|---|---|---|---|
|
7-18-0000 -
1-20-0490
2D בחה מבח |
7-18-0000 -
1-09-0203
2d בחג פבח |
7-18-0000 -
1-09-0203
2d בחג פבח |
7-18-0000 -
1-09-0203
2d בחג פבח |
|
1-20-0491 -
2-17-1079
2F בשז מבש |
1-09-0204 -
2-17-1079
2f בשה פבש |
1-09-0204 -
2-15-0588
2f בשה פבש |
1-09-0204 -
2-15-0588
2f בשה פבש |
|
2-18-0000 -
3-17-1079
3R גכז מגכ |
2-18-0000 -
3-09-0203
3r גכה פגכ |
2-15-0589 -
3-09-0203
3r גכה פגכ |
2-15-0589 -
3-09-0203
3r גכה פגכ |
|
3-18-0000 -
4-11-0694
5D החא מהח |
3-09-0204 -
5-09-0203
5r הכז פהכ |
3-09-0204 -
5-09-0203
5r הכז פהכ |
3-09-0204 -
5-09-0203
5r הכז פהכ |
|
4-11-0695 -
5-17-1079
5F השג מהש |
5-09-0204 -
5-17-1079
5f השא פהש |
5-09-0204 -
5-17-1079
5f השא פהש |
5-09-0204 -
5-17-1079
5f השא פהש |
|
5-18-0000 -
6-20-0490
7D זחג מזח |
5-18-0000 -
6-09-0203
7d זחא פזח |
5-18-0000 -
6-09-0203
7d זחא פזח |
5-18-0000 -
6-00-0407
7d זחא פזח |
|
6-20-0491 -
7-17-1079
7F זשה מזש |
6-09-0204 -
7-17-1079
7f זשג פזש |
6-09-0204 -
7-17-1079
7f זשג פזש |
6-00-0408 -
7-17-1079
7f זשג פזש |
We now know how to calculate Rosh Hashanah and its secular date for any Hebrew year. However, you may want to calculate the secular date for other Hebrew dates, such as other holidays or a date of death from a Hebrew tombstone. This can be complicated because there are variations in the length of two months (Cheshvan and Kislev, as discussed above) and the possibility that it is a leap year, but those three pieces are all in the keviya, so this is manageable.
Start by calculating the Rosh Hashanah date and keviya for the desired year. If you don't know the Hebrew year number, remember that the Hebrew year begins with Rosh Hashanah in Tishri, which is in September or October. Add 3761 to the secular year for the September before the date you want. For example, to get the secular date for Passover in 2026, start with Rosh Hashanah for 5786 (Rosh Hashanah of that Hebrew year is in the fall of 2025, 2025 + 3761 = 5786). For years on a tombstone, remember that the first Hebrew digit is not written and add 5000 to the Hebrew year number written on the tombstone. You're not likely to find -- or be able to read! -- tombstones before the year 5000, which is secular year 1239. If a tombstone gives the year of death as תשסא, which has the value of 761, that's actually 5761, which started in the year 2000.
Depending on where the date you want lands, you may need to make a note of the number of days in Cheshvan (30 in a Shaleim, complete year; otherwise 29), Kislev (29 in a Chaseir, deficient year; otherwise 30) and whether it is a leap year (add 30 days). I will refer to these three numbers as Cheshvan Days (29 or 30), Kislev Days (29 or 30) and Leap Days (0 or 30). Then use the calculations below for the desired month
The form below uses the functions above to calculate the dates of major Jewish holidays for any Hebrew year after 5731 (1970/71).
You may want to start with a secular date and find out what day it is on the Hebrew calendar, such as calculating a person's Hebrew birthday or yahrzeit or what day today is.
First, calculate Rosh Hashanah and keviya for the Hebrew year. If the date is before September, assume the Hebrew year is the secular year + 3760 (Rosh Hashanah is never before September... at least, not back to the 1700s) If the date is September or later, try the Hebrew year that is the secular year + 3761. If the resulting Rosh Hashanah for year + 3761 is before your date ... if all you care about his the Hebrew date and not any other information, you can just work with the negatives, because the six months before Rosh Hashanah are all constant length. The code that I've attached calculates dates a couple of months before Rosh Hashanah and a month into the following year. If you need more information then calculate the Rosh Hashanah and keviyah for the secular year + 3760.
Next, you will need three pieces of information that you get from the keviya:
Then you calculate the number of days between the secular date of Rosh Hashanah you calculated and the secular date you want to convert to a Hebrew. I actually add a day to this difference to include the starting date (Rosh Hashanah) and call it the day of year (DoY). Details of the calculation are in the attached code and it's pretty straighforward, and I couldn't do a much better job to explain it. If the DoY is less than the end of a month, it's in that month and subtract the number of days in previous months to get the day of the month. The form below uses the attached code to calculate Hebrew dates for secular dates. I adjusted it to allow dates back to 1900.
At one time, the accuracy of the Jewish calendar was proverbial. But how accurate is it really?
The months are remarkably accurate. The average lunar month on the Jewish calendar is 29d 12h 793p. The average synodic month as calculated by modern astronomers (the full cycle of moon phases) is 29d 12h 44m 2.8s, that is, 29d 12h 792.84p. so the variation is less than two tenths of the smallest unit of measurement recognized by the system, about half of a second. Of course, those lost half-seconds do add up: within the 1700 years isnce the calendar was created, it's gotten off by about 15 minutes. You can see the accuracy if you compare an astronomical calendar of moon phases to the months on a Jewish calendar: Rosh Chodesh (the first of the month) is a day or two after the astronomical new moon, which is what it should be because the astronomical new moon is the darkest point and Rosh Chodesh is when the moon first becomes visible.
How well does the calendar correspond to the solar year? The rabbis recognized long ago that the calendar gains 1h 485p in every 19-year cycle, adding up to a day every 300 years or so. This was important to the rabbis in scheduling certain rituals that are based on the solar year rather than the lunar year. We can see this effect when we examine the secular dates of Rosh Hashanah over time.
Rabbi Hillel II developed the Jewish calendar in the Jewish year 4119. Using his calendar methods as described above, and artificially assuming that the Gregorian calendar we use today was in effect at that time, the date of Rosh Hashanah ranged from August 29 to September 28 between the years 4100 and 4200 (the 42nd century). In the present Jewish century (the 58th), the dates of Rosh Hashanah range from September 5 to October 5, a gain of 6 or 7 days. This is considerably more accurate than the Julian calendar used by Christians in Rabbi Hillel's time (which had to be corrected by 11 days a few centuries ago), but you can see that it is gaining some time.
The discrepancy in the Jewish calendar, however, is still less than a lunar month and is therefore as accurate as it is possible to be in a lunisolar calendar, and it will be thousands of years until the discrepancy reaches a full month. The rabbis were aware of the problem, but were quite confident that a new Sanhedrin would be established long before this discrepancy becomes problematic. We still have thousands of years to go.
The book that most people recommend for learning about the Jewish calendar is Rabbi Nathan Bushwick's Understanding the Jewish Calendar. I ordered this book while I was writing this page; it took about a month to arrive, and I confess I was a bit disappointed by it. About half of the book was basic astronomy that I learned in fourth grade, and most of the calendar calculations I had learned before the book arrived. Nevertheless, the book did have some interesting insights and thorough citation to Torah, Talmud and Rambam that you may find useful or interesting.
Current Calendar
Jewish Calendar
Numerical Values